The evaluated cross-section data constitute an array of points (E_i,σ_i). Taking into account that the points are dense enough on energy for the cross-section to be smoothed by the spreading caused by a spectroscopy system resolution the energy spectrum for a uniform thick target is constructed in a following way.

First the energy E_i is assigned to be equal to the energy E₁ which a projectile of the initial energy E₀ penetrating a sample possesses at the depth x_i, where the interaction characterized by the cross-section σ_i occurs. Then the depth x_i and the corresponding energy E_3i registered by a detector are calculated. In order to speed up the calculations stopping power was approximated by a following function

,

which can be integrated analytically. The corresponding formulas are as follows:

,

,

,

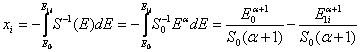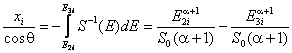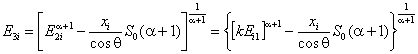where θ is a scattering angle, E₂ is the energy of the outgoing particle immediately after an interaction and k is a kinematical factor.

The interaction yield Y₁(E_1i) at the depth x_i is obtained by a convolution of the cross-section with the beam spreading function which is assumed to be represented by Bohr’s straggling theory:

,

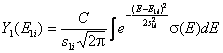where

with Z_t and Z_p standing for the charges of the target nucleus and the projectile respectively, and C is atomic concentration.

The yield of the registered particles Y₃(E_3i) is calculated as a convolution of the yield Y₁(E_1i) with the Gaussian spreading function, the variance including both straggling on the way out and the detector resolution:

.

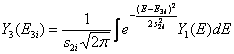The yield per a MCA channel of width ΔE₃ is

,

where Q and Ω are the number of projectiles and the detector solid angle respectively, and

.

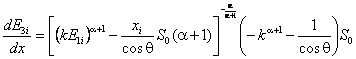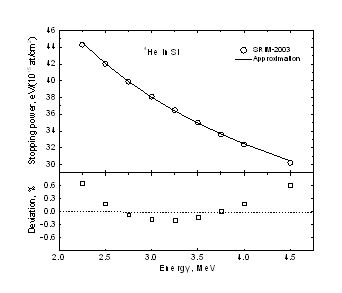
The stopping power approximation used in the calculations is accurate up to tenths of percent in the energy range of interest as can be seen from the following figure. It is worth noting that the discrepancy between different systematics of the stopping power data is much greater.